Pentominoes are a classic puzzle and mathematical object with a surprising amount of depth. Here’s a comprehensive overview, covering their history, properties, variations, and applications:
1. What are Pentominoes?
- Definition: Pentominoes are polyominoes of order 5. That means they are shapes formed by joining five congruent squares edge-to-edge.
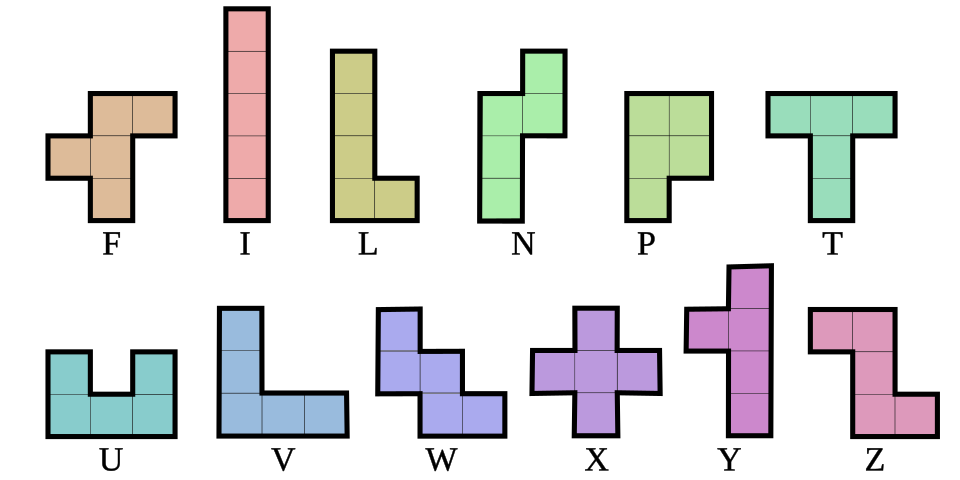
- The 12 Pentominoes: There are exactly 12 distinct pentominoes, considering rotations and reflections as the same shape. They are commonly named after letters they resemble: F, I, L, N, P, T, U, V, W, X, Y, Z.
- Key Characteristics:
- Each pentomino covers exactly 5 square units.
- They are connected edge-to-edge, not corner-to-corner.
- Rotations and reflections don’t create new pentominoes.
2. History & Discovery
- Early Mentions: The idea of polyominoes (shapes made of squares) dates back to ancient times, but the systematic study of pentominoes began in the mid-20th century.
- Solomon W. Golomb (1953): Mathematician Solomon W. Golomb is credited with popularizing pentominoes. He wrote a paper titled “Polyominoes” and developed many of the puzzles and problems associated with them. He also coined the term “pentomino.”
- Commercialization: In the 1950s and 60s, pentomino puzzles became commercially successful, often sold as a set of wooden pieces. They were marketed as educational toys to develop spatial reasoning skills.
3. Mathematical Properties & Problems
Pentominoes are a rich source of mathematical exploration. Here are some key areas:
- Tiling: A major challenge is to tile a given region with pentominoes without overlaps or gaps.
- Rectangle Tiling: The most famous problem is tiling a 6×10 rectangle with all 12 pentominoes. There are 2339 different solutions (not counting rotations and reflections).
- Other Shapes: Tiling other shapes (like squares, triangles, or irregular polygons) with pentominoes is also studied.
- Covering: Can a given shape be completely covered by pentominoes?
- One-Sided Tiling: Tiling a region so that the pentominoes can only be placed on one side of the region.
- Fixed vs. Free Pentominoes:
- Fixed Pentominoes: The pentominoes are placed on a grid with specific constraints (e.g., certain squares must be covered).
- Free Pentominoes: The pentominoes can be placed anywhere on the grid.
- Number of Solutions: Finding the number of possible arrangements for tiling or covering problems is a complex combinatorial challenge.
- Coloring Problems: Coloring the squares of a pentomino with a limited number of colors, subject to certain rules.
4. Variations & Extensions
- Polyominoes: The general term for shapes formed by joining squares edge-to-edge.
- Tetrominoes (order 4): Shapes made of 4 squares (e.g., I, O, T, L, J, S, Z). These are the pieces in the game Tetris.
- Hexominoes (order 6): Shapes made of 6 squares.
- Heptominoes (order 7): Shapes made of 7 squares, and so on.
- Polyiamonds: Similar to polyominoes, but formed by joining equilateral triangles edge-to-edge.
- Polycubes: Formed by joining cubes edge-to-edge in 3D.
- Irregular Pentominoes: Shapes formed by joining five congruent non-square shapes edge-to-edge.
5. Applications & Uses
- Education: Pentominoes are excellent tools for teaching:
- Spatial Reasoning: Visualizing and manipulating shapes.
- Problem Solving: Developing strategies to find solutions.
- Geometric Concepts: Area, perimeter, symmetry, and transformations.
- Logical Thinking: Deduction and pattern recognition.
- Computer Science: Algorithms for tiling and covering problems are used in areas like:
- Packing Problems: Optimizing the arrangement of objects in a limited space.
- Pattern Recognition: Identifying shapes and patterns in images.
- Game Design: Pentominoes have inspired various games and puzzles.
- Art & Design: Pentominoes can be used to create interesting patterns and designs.
6. Resources for Further Exploration
- Pentomino configurations and solutions: https://isomerdesign.com/Pentomino/ – A comprehensive website with puzzles, solutions, and information.
- Wikipedia – Pentomino: https://en.wikipedia.org/wiki/Pentomino
- MathWorld – Pentomino: https://mathworld.wolfram.com/Pentomino.html
- Online Pentomino Solvers: Several websites offer tools to help solve pentomino puzzles.
In conclusion, pentominoes are more than just a fun puzzle. They are a fascinating mathematical object with a rich history, challenging problems, and diverse applications. Whether you’re a mathematician, educator, or simply someone looking for a stimulating brain teaser, pentominoes offer something for everyone.